Troisième
Triangles semblables
Définitions
Pour montrer que deux triangles sont semblables il suffit de montrer que deux angles d'un triangle soient égaux à deux angles d'un autre triangle. En effet, puisque la somme des angles d'un triangle est égale à 180°, si deux angles sont deux à deux de même mesure, il en est de même pour le troisième angle de chaque triangle.
Exemple :
 BAC
BAC
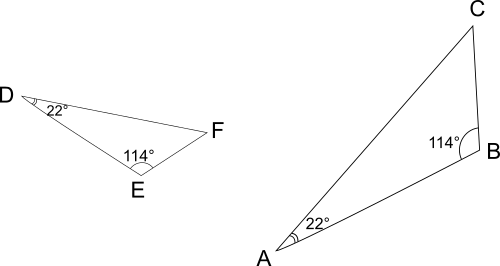
BA'C=ED'F=22°
DE'F=AB'C=114°
ABC et DEF ont deux angles égaux deux à deux donc ils sont semblables.
Remarque : on verifie facilement par le calcul que les deux derniers angles ont bien la même mesure :
AC'B=180 - 114 - 22 = 44° et
DF'E=180 - 114 -22 = 44°
À retenir :
Lorsque deux triangles sont semblables :
• Les angles égaux sont dits homologues
• Les côtés opposés à des angles égaux sont dits homologues
• Les sommets des angles égaux sont dits homologues
Troisième
Triangles semblables
Définitions
Pour montrer que deux triangles sont semblables il suffit de montrer que deux angles d'un triangle soient égaux à deux angles d'un autre triangle. En effet, puisque la somme des angles d'un triangle est égale à 180°, si deux angles sont deux à deux de même mesure, il en est de même pour le troisième angle de chaque triangle.
Exemple :
 BAC
BAC
BA'C=ED'F=22°
DE'F=AB'C=114°
ABC et DEF ont deux angles égaux deux à deux donc ils sont semblables.
Remarque : on verifie facilement par le calcul que les deux derniers angles ont bien la même mesure :
AC'B=180 - 114 - 22 = 44° et
DF'E=180 - 114 -22 = 44°
À retenir :
Lorsque deux triangles sont semblables :
• Les angles égaux sont dits homologues
• Les côtés opposés à des angles égaux sont dits homologues
• Les sommets des angles égaux sont dits homologues

